|
Formulas
In this section, the formulas used for
this article will be shown. These are excerpts from my personal
notes I wrote down in order to prepare this article. Since
these notes covered a dozen of pages or so in Word format,
I will try to shorten this as much as possible. Most equations
have been numbered for reference purpose. But not all will
necessarily be presented. So some equation numbers may be
missing, while other will appear out of sequence.
Size Calculations
These are the original Farless equations
for calculating size:
| O.D.
= 2R |
R
= R1 + H |
| R1
= R2 cos ½ a
|
I.D.
= 2 R2 |
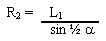 |
L1
= ½ (L - H cos a)
|
| a
= 360° / N, where N is the number of sides |
The formula for L1 needs to
be adjusted to work for any number of sides. For an 8-sided
spar, the V-notch uses equal 45-degree angles. At 45 degrees,
the sine and cosine have the same value. So in this particular
case, the formula will work with either the sine or cosine
function. For all possible configurations, we have to use
the sine function for the formula to work:
|
L1 = ½ (L - H sin a)
|
revised equation |
All the other formulas stay the same.
By combining all the "intermediate" values (R1,
R2 and L1), a few simplifications
were possible. The final revised equation for calculating
O.D. is:
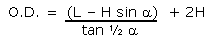 |
Equation 1 |
And the final revised equation for I.D.
is:
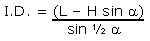 |
Equation 2A |
By replacing "H" with "K", these equations
become:
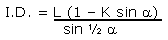
|
Equation 2B |
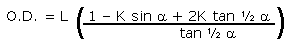
|
Equation 4A |
From these last two equations, we can
extract a lot of useful information. The long section between
brackets in Equation 4A is in fact the value for ratio M:
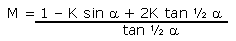 |
Equation 22 |
Here is the formula for calculating ratio
K from ratio A:
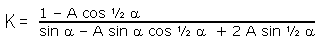
|
Equation 21A |
For a round exterior, the theoretical
minimum and maximum limits for the staves' thickness ratio
K are:
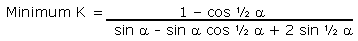
|
|
Equation 19 |
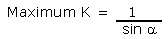
|
Equation 20 |
For a polygon exterior, the minimum K
is zero!
One side note, here: below is an alternate
equation for size I had figured out on my own. But it only
works for an 8-sided spar. For any other configuration,
it would have to be scrapped and re-written from scratch.
The approach used in the Farless equations is more universal.
The value for the angle (alpha), in the revised equations
presented here, automatically handles a different number
of sides. That's why this alternate equation is now obsolete.
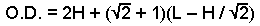
|
|
Obsolete alternate equation: for 8-sided spars only
|
Weight saving compared to a solid spar of the
same size
These formulas are more accurate than
the first approximation presented in the previous article
by David Farless. But they are substantially more complex.
The first approximation, in terms of weight saving, was:
Weight Saving (%) = 100 ( I.D. /O.D.) 2
In order to compare spars made up of a different number
of sides, the weight saving must be defined as:
Weight Saving (%) = 100 ( Empty Area / Solid Round Area
)
The complete formula that fits this definition is:
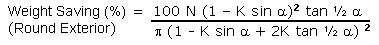
|
|
Equation 9B |
The definition and formula for a polygon
exterior are actually more complex than a round exterior:
The relative mass for a hollow polygon, compared to a solid
(included) circle is:
Relative Mass = ( Exterior Polygon Area - Empty Area ) /
Circle Area
The weight saving (in percent) is:
Weight Saving (Polygon)(%) = 100 ( 1 - Relative Mass)
And the complete formula is:
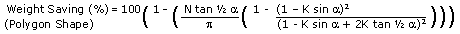
|
 (Click
to enlarge) (Click
to enlarge) |
Equation
10 |
Strength Loss
For a round exterior spar, the strength
loss is defined as:
Strength Loss (%) = 100 ( I.D. / O.D. ) 4
Using the values of I.D and O.D. defined in equations 2B
and 4A we obtain the following formula:
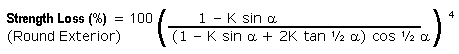
|
|
Equation 11 |
For a polygon outside shape, the outside
diameter used is the minimum value. The minimum outside
diameter is the same value as O.D. for a round exterior.
Since the ratio (I.D./O.D.) is constant all around, the
worst case figure is calculated using the minimum I.D. as
well. The minimum inside diameter is twice R1 (see Figure
1).
Strength Loss (%) = 100 ( minimum I.D. / O.D. ) 4
= 100 ( I.D. cos ½ a / O.D. ) 4
Strength Loss (%) = 100 ( A cos ½ a ) 4
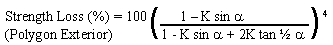
|
|
Equation 12 |
Size increase required for same strength as solid
spar (Round Exterior)
This is kind of the inverse of the strength
loss formula.
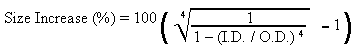
|
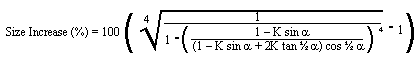
|
 (Click
to enlarge) (Click
to enlarge) |
Equation
15 |
Size increase required for same strength as solid
spar (Polygon Exterior)
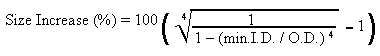
|
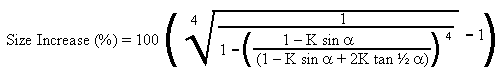
|
|
Equation 16 |
Weight Saving for the bigger hollow spar (Round
Exterior)
This is the weight saving equation for
a bird's mouth spar having a strength equivalent to a solid
round spar. The next two equations would just be too long
to show in their fully developed form.
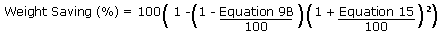
|
|
Equation 17 |
Weight saving for the bigger hollow spar (Polygon
Exterior)
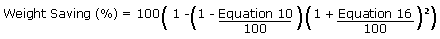
|
|
Equation 18 |
Outside Waste
The next two equations fall in the category:
"nice to know but way too much trouble to use!" The definitions
are understandable, but the equations needed to fit the
definitions are so long, they have to be broken in segments
to work in a spreadsheet! The outside waste that must be
removed for a round bird's mouth spar is defined as:
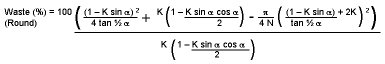
|
 (Click
to enlarge) (Click
to enlarge) |
Equation
13 |
The outside waste to be removed for a
polygon exterior is defined as:
And the formula for this is:
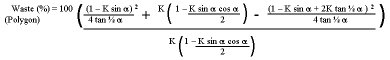
|
 (Click
to enlarge) (Click
to enlarge) |
Equation
14 |
Click here
to go the data tables. |

